Pengertian Matriks dan Jenis Matriks | Apa yang dimaksud dengan matriks?
Matriks adalah susunan sekelompok bilangan dalam suatu jajaran berbentuk persegi panjang yang diatur berdasarkan baris dan kolom dan diletakkan antara dua tanda kurung. Tanda kurung yang digunakan untuk mengapit susunan anggota matriks tersebut dapat berupa tanda kurung biasa atau tanda kurung siku. Setiap bilangan pada matriks disebut elemen (unsur) matriks. Kumpulan elemen yang tersusun secara horizontal
disebut baris, sedangkan kumpulan elemen yang tersusun secara vertikal
disebut kolom. Suatu matriks yang memiliki
m baris dan
n kolom disebut matriks
m x n dan disebut sebagai matriks yang memiliki orde
m x n. Penulisan matriks menggunakan huruf kapital dan tebal. Pembahasan
tentang matriks banyak ditemukan dalam ilmu Matematika.
 |
| Pengertian Matriks dan Jenis Matriks |
Matriks terbagi menjadi beberapa jenis, yaitu matriks persegi, matriks kolom, matriks baris, matriks transpose, matriks diagonal, matriks segitiga atas dan bawah, matriks nol, matriks simetri, dan matriks identitas. Berikut ini penjelasan lengkap tentang jenis-jenis matriks tersebut:
Matriks Persegi
Matriks persegi adalah matriks yang mempunyai banyak baris dan banyak kolom yang sama. Secara umum, matriks persegi berordo n x n. Contoh matriks persegi: |
| Contoh Matriks Persegi |
Matriks Kolom
Matriks kolom adalah matriks yang hanya mempunyai satu kolom. Secara umum, matriks kolom berordo m x 1. Contoh matriks kolom: |
| Contoh Matriks Kolom |
Matriks Baris
Matriks baris adalah matriks yang hanya mempunyai satu baris. Secara umum, matriks baris berordo 1 x n. Contoh matriks baris:
 |
| Contoh Matriks Baris |
Matriks Transpose
Matriks transpose
Am x n yang selanjutnya dinotasikan dengan
A� adalah matriks berordo n x m dengan baris-barisnya adalah kolom-kolom matriks
Am x n. Contoh matriks transpose, misalkan terdapat matriks A:
maka, transpose matriks A adalah:
Matriks Diagonal
Matriks diagonal berasal dari matriks persegi. Matriks persegi dikatakan sebagai matriks diagonal jika elemen-elemen selain elemen diagonal utamanya adalah nol. Contoh matriks diagonal:
 |
| Contoh Matriks Diagonal |
Matriks Segitiga Atas dan Matriks Segitiga Bawah
Matriks segitiga atas dan matriks segitiga bawah dapat berasal dari matriks persegi. Suatu matriks persegi disebut matriks segitiga atas jika semua elemen di bawah diagonal utamanya bernilai nol. Sebaliknya, jika semua elemen di atas diagonal utamanya bernilai nol, maka matriks persegi itu disebut matriks segitiga bawah. Contoh Matriks Segitiga atas dan Matriks Segitiga Bawah:
Matriks A adalah matriks segitiga atas, sedangkan matriks B adalah matriks segitiga bawah.
Matriks Simetri
Misalkan terdapat matriks A. Matriks A disebut matriks simetri jika A� = A atau setiap elemen pada matriks A yang letaknya simetris terhadap diagonal utama bernilai sama, yaitu aij = aji dengan i tidak sama dengan j. Contoh matriks simetri, misalkan:
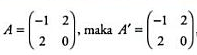 |
| Sehingga A adalah matriks simetri |
Matriks Nol
Suatu matriks dikatakan matriks nol jika semua elemen dari matriks tersebut adalah nol. Contoh matriks nol:
 |
| Contoh matriks nol |
Matriks Identitas
Matriks identitas adalah matriks diagonal yang semua elemen pada diagonal utamanya adalah 1.Matriks identitas biasanya dinotasikan dengan I. Contoh matriks indentitas:
 |
| Contoh matriks indentitas |
Sekian uraian tentang
Pengertian Matriks dan Jenis Matriks, semoga bermanfaat.




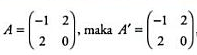





0 Comment: